The Pendubot

Pendubot Movie (1.7M)

Description

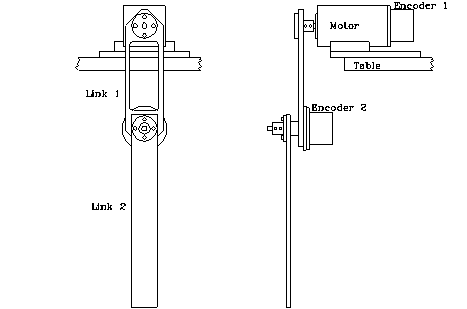
The Pendubot, short for PENDUlum RoBOT, is an electro-mechanical (Mechatronic) system consisting of two rigid links interconnected by revolute joints. The first joint is actuated by a DC-motor and the second joint is unactuated. Thus the second link is a simple pendulum whose motion can be controlled by actuation on the first link. The Pendubot is similar in spirit to the classical inverted pendulum on a cart or the more recent rotational inverted pendulum.

Swing up halfway (0.4M)			Swing up control(0.5M)			Robustness (1.7M)
Disturbance (0.8M)			Stability demonstration (2.4M)			Less stable gains (2.2M)

Due to the nonlinear dynamic coupling between the two links, the Pendubot possesses some unique features and challenges for control research and education not found in other devices. Using the Pendubot one can investigate system identification, linear control, nonlinear control, optimal control, learning control, robust and adaptive control, fuzzy logic control, intelligent control, hybrid and switching control, gain scheduling, and other control paradigms. One can program the Pendubot for swingup control, balancing, regulation and tracking, identification, gain scheduling, disturbance rejection, and friction compensation -- to name just a few of the applications.

An unstable equilibrium stabilized through feedback

q1=pi/4, stabilized

q1=pi/2, stabilized

Underactuated mechanical systems generally have equilibria which depend on both their kinematic and dynamic parameters. If the Pendubot is mounted so that the joint axes are perpendicular to gravity, then there will be a continuum of equilibrium configurations, each corresponding to a constant value of the input torque. This feature is pedegogically useful in several ways, to illustrate how the Taylor series linearization is operating point dependent and for teaching controller switching and gain scheduling. One can also easily understand physically how the linearized system becomes uncontrollable at q₁=0, ± pi (the reference position for q₁is horizontal), in the position shown below.